Question

If the range of the function y = f(x) is y ≥ 11, y ∈ R, then the range of the new function g(x) = f(x + 2) - 3 is

Answer 1

y ≥ 8

Step-by-step explanation:

Note that if f(x) is transformed into f(x + a) - b

The original functions is shifted a units to the left and b units downward.

Horizontal shifting will not affect the range of the function, only vertical shifting will change its range.

From the given, g(x) is the transformation of f(x) with

`g(x)=f(x+2)-3_{}`

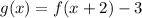
f(x) is shifted 2 units to the left and 3 units downward, we will disregard the horizontal shifting.

Since f(x) has a range of y ≥ 11, and g(x) is 3 units downward, the range will also move 3 units downward.

y ≥ 11 - 3

The answer is y ≥ 8