Question

In the figure below line DE is parallel to line FG and transversal AG

Answer 1

Answer: The answer is 147° and 33°.

Step-by-step explanation: We are given a figure in which the line DE is parallel to the line FG and AG is a tranversal. We are to find the value of 'x' and 'y' from the figure.

Also, given that

∠ABE = (5y - 18)°.

We can see from the figure that ∠DBG and ∠ABE are vertically opposite angles, so they must be equal.

That is,

`\angle DBG=\angle ABE\\\\\Rightarrow x=5y-18\\\\\Rightarrow 5y-x=18.~~~~~~~~~~~~~~~(i)`

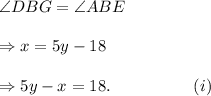
Also, since ∠DBG and ∠FGB are interior angles on the same side of the transversal, so their sum is 180°.

That is

`\angle DBG+\angle FGB=180^\circ\\\\\Rightarrow x+y=180.~~~~~~~~~~~~~~~~~(ii)`

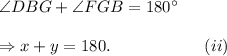
Adding equations (i) and (ii), we get

`y+5y=18+180\\\\\Rightarrow 6y=198\\\\\Rightarrow y=33,`

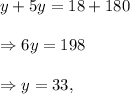
and from equation (ii), we get

`x=180-33=147.`

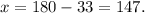
Thus, x° = 147° and y° = 33°.