We are asked to determine the tension in the system. To do that we will add the vertical forces on the 50g mass using the following free-body diagram:
Where:
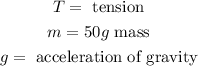
Adding the vertical forces we get (taking downward forces to be positive and upward negative):
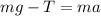
Where "a" is the acceleration of the system.
If we divide by mass "m" we get:
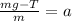
Now, we add the horizontal forces for the 250g mass using the following free-body diagram:
Where:
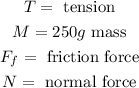
Now, we add the horizontal forces we get:
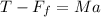
The friction force is given by:
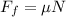
Since the object is not accelerating in the vertical direction this means that the normal force is equivalent to the weight of the 250g mass, therefore, we have:
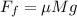
Substituting in the sum of forces we get:

Now, we divide both sides by the mass "M":
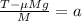
Since the acceleration is the same for both masses we can set them equal together and we get:
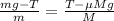
Now, we solve for the tension "T". First, we distribute both denominators:
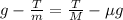
Now, we add T/m:
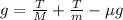
Now, we add the coefficient of friction and the gravity to both sides:
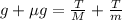
Now, we take "T" as a common factor:
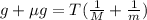
Now, we divide both sides by the factor:
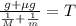
Now, we substitute the values:

Solving the operations:
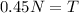
Therefore, the force of tension is 0.45 N.
Now, we determine the acceleration by substituting the value of the force of tension in any of the two formulas for acceleration:
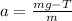
Substituting the values:

Solving the operations:
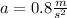
Therefore, the acceleration is 0.8 m/s/s.
The net force on the system is given by Newton's second law:
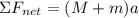
Where "M + m" is the total mass of the system and "a" is the acceleration of the system. Substituting the values we get:
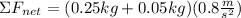
Solving the operations:
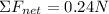
Therefore, the net force is 0.24 N.