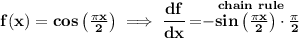
now, what is the value of the derivative at any extrema on the original function? well, by definition, if the original function has an extrema anywhere, the derivative will be the derivative of a horizontal tangent line to it, and by definition it'll be 0.