Question

What is the equation of this trend line?

Enter your answers by filling in the boxes.

Answer 1

`\sf N = \boxed{-2}\;M + \boxed{110}`

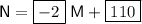
Explanation:

A trend line, also known as a line of best fit or regression line, is a straight or curved line that represents the general direction or pattern of a set of data points in a scatter plot or graph.

Trendlines are commonly used to identify patterns, make predictions, and understand the overall behavior of a dataset, and provide a visual representation of the underlying trend in the data.

The independent variable of a scatter plot is always drawn along the horizontal axis. The dependent variable of a scatter plot is always drawn along the vertical axis.

The trend line in the given scatter plot is a straight line with a negative slope. It shows the relationship between the variables M and N.

The trend line crosses the y-axis at (0, 110) and crosses the x-axis at (55, 0).

To find the slope of the trend line, substitute the two points on the line into the slope formula:

`\textsf{Slope $(m)$}=(y_2-y_1)/(x_2-x_1)=(0-110)/(55-0)=(-100)/(55)=-2`

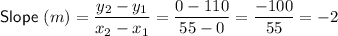
Substitute the found slope, m = -2, and the y-intercept, b = 110, into the slope-intercept formula, y = mx + b:

`y=-2x+110`

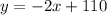
As variable M is the independent variable, substitute x = M.

As variable N is the dependent variable, substitute y = N.

Therefore, the equation of the given trend line is:

`\boxed{\sf N=-2M+110}`