Question

What is the range of the function f(x) = |x – 5| – 3? R: f(x) > 2 R: f(x) ∈ ℝ R: f(x) ∈ ℝ R: f(x) ∈ ℝ

Answer 1

R: f(x) ≥ –3

Explanation:

I got it right on the test.

Answer 2

Given,

The expression is,

`f(x)=|x-5|-3`

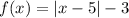
Required

The range of the function.

The range of the function is calculated by taking,

`\begin{gathered} f(5)=|5-5|-3=-3 \\ f(4)=\lvert4-5\rvert-3=-2 \\ f(6)=\lvert6-5\rvert-3=-2 \\ f(3)=\lvert3-5\rvert-3=-1 \\ f(7)=\lvert7-5\rvert-3=-1 \end{gathered}`

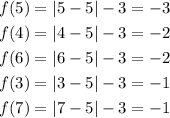
From the above data , it is clear that the set of the output values have the values greater than or equal to -3.

Hence, range of the function is R: f(x) ∈ ℝ .