Answer: 29524
Explanation:
Given geometric sequence : 1, 3, 9, …........................
First term of G.P.
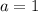
Second term of G.P.
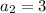
Common ratio =

We know that the sum of the geometric sequence with n terms is given by :-
 for |r|>1
for |r|>1
Substitute a = 1 , r =3 and n=10 , we get
