Question

The sum of the circumference of a circle and the perimeter of a square is 16. find the dimensions of the circle and square that produce a minimum total area. (let x be the length of a side of the square and r be the radius of the circle.)

Answer 1

Let r = the radius of the circle.
Let x = the length of a side of the square.

The sum of the circumference of the circle and the perimeter of the square is 16.
Therefore
2πr + 4x = 16
That is

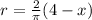
`r = (2)/( \pi ) (4-x)` (1)

The combined area of the circle and the square is

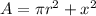
`A = \pi r^(2) + x^(2)` (2)

From (1), obtain

`A = \pi . (4)/( \pi ^(2))(4-x)^(2) + x^(2) = (4)/( \pi ) (4-x)^(2)+x^(2)`

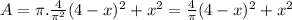
In order for A to be minimum, A' = 0.
That is,

`- (8)/( \pi ) (4-x)+2x=0 \\x(2+ (8)/( \pi ) ) = (32)/( \pi ) \\ x =2.2404`
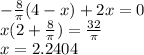
The second derivative should be positive in order for A to be minimum.
A'' = 8/π + 2 > 0 , so the condition is satisfied.
The graph shown below confirms this.

From (1), obtain
r = (2/π)*(4 - 2.2404) = 1.1202

Answer:
r = 1.12 and x = 2.24