Given that in a national highway Traffic Safety Administration (NHTSA) report, data provided to the NHTSA by Goodyear stated that the mean tread life of a properly inflated automobile tires is 45,000 miles. Suppose that the current distribution of tread life of properly inflated automobile tires is normally distributed with mean of 45,000 miles and a standard deviation of 2360 miles.
Part A:
Find the probability that randomly selected automobile tire has a tread life between 42,000 and 46,000 miles.
The probability that a normally distributed data set with a mean, μ, and standard deviation, σ, is between two numbers, a and b is given by:
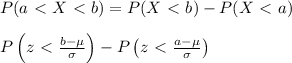
Given that the the mean tread life of a properly inflated automobile tires is 45,000 miles a standard deviation of 2360 miles.
The probability that randomly selected automobile tire has a tread life between 42,000 and 46,000 miles is given by:
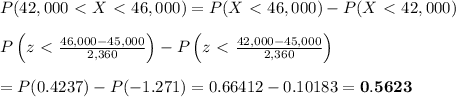
b. Find the probability that randomly selected automobile tire has a tread life of more than 50,000 miles.
The probability that a normally distributed data set with a mean, μ, and standard deviation, σ, is greater than a numbers, a, is given by:
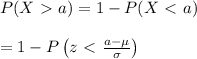
Given that the the mean tread life of a properly inflated automobile tires is 45,000 miles a standard deviation of 2360 miles.
The probability that randomly selected automobile tire has a tread life of more than 50,000 miles is given by:

Part C:
Find the probability that randomly selected automobile tire has a tread life of less than 38,000 miles.
The probability that a normally distributed data set with a mean, μ, and standard deviation, σ, is less than a numbers, a, is given by:
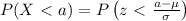
Given that the the mean tread life of a properly inflated automobile tires is 45,000 miles a standard deviation of 2360 miles.
The probability that randomly selected automobile tire has a tread life of less than 38,000 miles is given by:
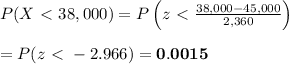
d. Suppose that 6% of all automobile tires with the longest tread life have tread life of at least x miles. Find the value of x.
The probability that a normally distributed data set with a mean, μ, and standard deviation, σ, is greater than a numbers, x, is given by:
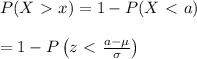
Given that the the mean tread life of a properly inflated automobile tires is 45,000 miles and a standard deviation of 2360 miles and that the probability that all automobile tires with the longest tread life have tread life of at least x miles is 6%.
Thus:
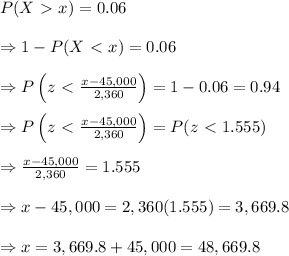
Therefore, the value of x is 48,669.8
e. Suppose that 2% of all automobile tires with the shortest tread life have tread life of at most x miles. Find the value of x.
The probability that a normally distributed data set with a mean, μ, and standard deviation, σ, is less than a numbers, x, is given by:
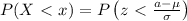
Given that the the mean tread life of a properly inflated automobile tires is 45,000 miles and a standard deviation of 2360 miles and that the probability that all automobile tires with the longest tread life have tread life of at most x miles is 2%.
Thus:
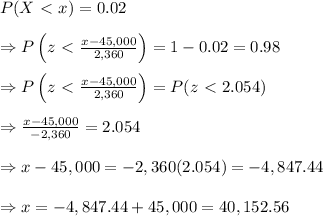
Therefore, the value of x is 40,152.56