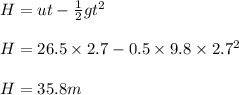Question

A toy projectile is fired from the ground vertically upward with an initial velocity of 26.5 m/s. The project arrives at its maximum altitude in 2.7s.

Determine the greatest height the projectile reaches. How do you know?

Answer 1

To work with projectile motion equations, it’s best to solve the equations in terms of x and y. In this problem, we know that we are working with only the y-axis because the projectile is launched vertically upwards with no angle. We can exclude working with our equations for the x-axis and look at the variables and equations we have for the y-axis.

Known variables along the y-axis
Viy = 26.5 m/s (initial velocity)
Vfy = 0 m/s (final velocity at max height)
ay = -g = 9.8m/s²
Siy = 0 m (toy launched from ground)
Sfy = ? = max height when t=2.7s
t = 2.7s

We can use equation Sfy = (Viy•t) - 1/2gt²
= (26.5•2.7) - 1/2(9.8)(2.7)²
= 35.83 m

Therefore, the greatest height the projectile reaches when launched from the ground with a velocity of 26.5m/s is 35.83m

Hope this helps!

Answer 2

35.8 m

Step-by-step explanation:

Given:

Initial Velocity u = 26.5 m/s

Time period t = 2.7 s

To find:

Maximum height H = ?

Solution:

The toy is projected vertically upward. So the motion is happening in y axis

When a projectile reaches its maximum height, at that point its velocity vill be zero

Using equations of motion we can find the height

`v^(2) =u^(2) -2gH\\\\0^(2) =26.5^(2) -2* 9.8 * H\\\\19.6H = 702.25\\\\H = 35.8 m`

Verification

`H = ut - (1)/(2) gt^(2)\\\\H = 26.5 * 2.7- 0.5 * 9.8 * 2.7^(2)\\\\H = 35.8 m`