Question

Hello i need help in this, someone pls!!!

Answer 1

The given ODE is

`(dy)/(dx) = (x)/(y)`

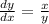
Let y² = x - v
Then

`2y (dy)/(dx) =1 - (dv)/(dx) \\\\ (dy)/(dx) = (1)/(2y) (1- (dv)/(dx) )`

Substitute in the original ODE.

`(1)/(2y) (1- (dv)/(dx)) = (x)/(y) \\\\ 1- (dv)/(dx) =2x \\\\ (dv)/(dx) =1-2x`

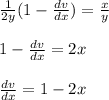
Integrate with respect to x to obtain
v = x - x² + b
Hence obtain
y² = x² + b

When y(x) passes through (0,0), obtain
b = 0
y² = x²
When y(x) passes through (1,0), obtain
0 = 1 + b => b = -1
y² = x² - 1
When y(x) passes through (0,1), obtain
1 = 0 + b => b = 1
y² = x² + 1

A graph of the three solutions is shown below.