Question

Based on a​ poll, 5050​% of adults believe in reincarnation. assume that 44 adults are randomly​ selected, and find the indicated probability. complete parts​ (a) through​ (d) below.

a. what is the probability that exactly 33 of the selected adults believe in​ reincarnation? the probability that exactly 33 of the 44 adults believe in reincarnation is

Answer 1

Answer is 0.096

Explanation:

Here 44 adults are randomly selected.

Each adult selected is independent of the other to believe in reincarnation.

Also there are only two outcomes, probability for success in each trial = 0.50

Hence X no of adults who believe in reincarnation is binomial with n =50 and p = 0.50

`a) P(X=23) = 50C23 (0.5)^(50) =0.096`

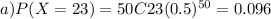
Working notes:

50C23 =108043253365600

0.5^50) = 8.8178x10^(-14)

Simplifying we get answer as 0.096

Answer 2

To solve this problem, we use the formula for binomial probability:

P = [n! / (n – r)! r!] p^r * q^(n – r)

where,

n = total number of adults = 4

r = number of adults who believe in reincarnation = 3

p = chance of believing in reincarnation = 50% = 0.50

q = 1 – p = 0.50

P = [4! / (4 – 3)! 3!] 0.50^3 * 0.50^(4 – 3)

P = 0.25 = 25%