Question

What is an mam dhe qet 58 JOO

Answer 1

To solve the exercise, first, we are going to write in numerical form the equation shown in fraction models:

`\begin{gathered} (4)/(10)+x=(88)/(100) \\ \text{ Because} \\ (4)/(10)\Rightarrow\text{ There are 4 shaded lines out of the 10 in total} \\ (88)/(100)\Rightarrow\text{ There are 88 shaded squares out of the 100 in total} \end{gathered}`

Now, you can solve the equation for x:

`\begin{gathered} (4)/(10)+x=(88)/(100) \\ \text{ Subtract }(4)/(10)\text{ from both sides of the equation} \\ (4)/(10)+x-(4)/(10)=(88)/(100)-(4)/(10) \\ x=(88)/(100)-(4)/(10) \end{gathered}`

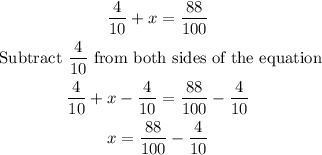
To subtract these fractions, you can amplify the fraction 4/10, that is, multiply by 10 in the numerator and denominator of the fraction:

`(4)/(10)=(4\cdot10)/(10\cdot10)=(40)/(100)`

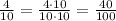
Now that both fractions have the same denominator, it is easier to subtract them, since it is enough to subtract their numerators. So, you have:

`\begin{gathered} x=(88)/(100)-(4)/(10) \\ x=(88)/(100)-(40)/(100) \\ x=(88-40)/(100) \\ x=(48)/(100) \\ \end{gathered}`

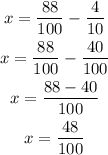
Therefore, the fraction that makes the equation true is

`(48)/(100)`

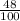
and the correct answer is option C.