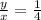Question

The graph shows a line and two similar triangles.

Answer 1

your first option y/x=1/4 is correct

Answer 2

Option (a) is correct.

The equation of the line is expressed using expression
`(y)/(x)=(1)/(4)`

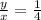
Explanation:

Given : The graph shows a line and two similar triangles.

We have to find the expression that finds the equation of line.

Since, given two triangles are similar.

So, Δ ABC ≅ Δ ADE

Thus, There corresponding sides are in same proportion.

`(AC)/(AD)=(CB)/(DE)= (AB)/(BE)`

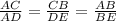
Substitute, we get,

`(1)/(y)=(4)/(x)= (AB)/(BE)`

Rearrange, we have,

`(1)/(4)=(y)/(x)= (AB)/(BE)`

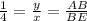
Also, finding slope of line AE,

Coordinate of B is (4,1) and Coordinate of A is (0,0)

Th equation of line is y = mx + c

Where, m is slope and c is x intercept

Since,
`m=(y_2-y_1)/(x_2-x_1)`

`m=(1-0)/(4-0)`

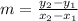
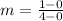
Simplify, we have,

`m=(1)/(4)`

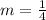
And c = 0

Thus, equation of line is
`y=(1)/(4)x`

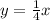
We re-writing we get,

`(y)/(x)=(1)/(4)`

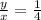
Thus, The equation of the line is expressed using expression
`(y)/(x)=(1)/(4)`