Question

A music website charges x dollars for individual songs and y dollars for entire albums. Person A pays $25.92 to download 6 individual songs and 2 albums. Person B pays $33.93 to download 4 individual songs and 3 albums. Write a system of linear equations that represents this situation.

Answer 1

Let
`x` equals to amount charged for downloading individual songs
`\Rightarrow`
`y` equals to amount charged for downloading an entire album.

Solve the system for
`y`:

`\left\{{{6x+2y = 25.92,}\atop{4x + 3y = 33.93;}}\right \left\{{{6x+2y = (648)/(25),}\atop{4x + 3y = (3393)/(100);}}\right \\\left\{{{6x+2y-2y = (648)/(25)-2y,}\atop{4x + 3y = (3393)/(100);}}\right \left\{{{6x = (648)/(25)-2y,}\atop{4x + 3y = (3393)/(100);}}\right \\\left\{{{x = (-25y+324)/(75),}\atop{4x + 3y = (3393)/(100);}}\right \left\{{{x = (-25y+324)/(75),}\atop{4(-25y+324)/(75) + 3y = (3393)/(100);}}\right`

`\left\{{{x = (-25y+324)/(75),}\atop{(4(-25y+324))/(75) * 300 + 3y * 300 = (3393)/(100) * 300;}}\right \left\{{{x = (-25y+324)/(75),}\atop{16(-25y+324)+900y = 10179;}}\right \\\left\{{{x = (-25y+324)/(75),}\atop{500y+5184 = 10179;}}\right \left\{{{x = (-25y+324)/(75),}\atop{500y = 4995;}}\right \\\left\{{{x = (-25y+324)/(75),}\atop{y = (999)/(100) = 9.99;}}\right`

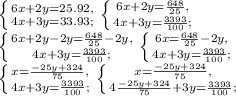
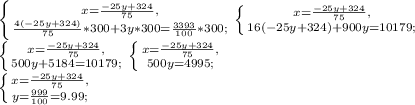
Solving the system for
`x` is unoptional since we already have the answer we've been looking for. Your answer is
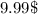
`9.99\$`.