Question

The function g(x) = –x2 + 16x – 44 written in vertex form is g(x) = –(x – 8)2 + 20. Which is one of the transformations applied to the graph of f(x) = x2 to change it into the graph of g(x) = –x2 + 16x – 44?

Answer 1

It was moved up 20 units

Answer 2

the graph of f(x) will be reflected over x axis, moved 8 units to the right and shifted 20 units up to get g(x)

Explanation:

The function
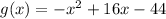`g(x) = -x^2 + 16x - 44` written in vertex form is
`g(x) = -(x - 8)^2 + 20`

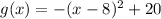
The parent function is f(x)=x^2

Now we compare parent function f(x) and g(x)

In g(x), negative sign at first

f(x) ----> -f(x) , the graph is reflected across x axis

f(x)-----> f(x-h), the graph will be transformed h units to right

f(x)----> f(x) +k , the graph will be transformed k units up

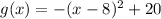`g(x) = -(x - 8)^2 + 20`, the graph of f(x) will be reflected over x axis, moved 8 units to the right and shifted 20 units up to get g(x)