Question

2.   Using the normal curve table, determine the area of the standard normal distribution that is less than the following z-scores:

a.   z = .30
b.   z = 1.75
c.   z = 2.42
d.   z = −.68
e.   z = −1.11
I need to see the answer and the formula doing this

Answer 1

The normal distribution pdf is

`f(x|\mu,\sigma ^(2) ) = (1)/(\sigma √(2 \pi ) ) e^{- ((x-\mu)^(2))/(2\sigma^(2))`
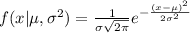
where
μ = population mean,
σ = population standard deviation

For a random variable x, the probability (area under the normal curve) is

`\int _(-\infty) ^(x) f(x | \mu. \sigma ^(2))} dx`

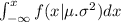
Define z = (x - μ)/σ.
Then
dx = σ (dz)
and the area under the curve transforms to

`\int _(-\infty) ^(z) (1)/( √(2 \pi ) ) e^{ - (z^(2))/(2) } dz`

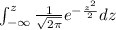
This integral is evaluated numerically (trapezoidal or Simpson's rule). For the lower limit, a value of z = -4 instead of ∞ is sufficient for good accuracy.

For example, with the trapezoidal rule, use a step size of h = 0.05.
Between z = -4 to z = 0.3, there are 87 values.
Calculate the function values as y₀, y₁, y₂, ..., y₈₇.
y₀ + y₈₇ = 0.3815
y₁+y₂+ ... +y₈₆ = 12.1664
The area is
A = (0.05/2)*(0.3815 + 2*12.1664) = 0.025*24.7142 = 0.6179.

Results for specified values of z are
(a) z = 0.30, Area = 0.6179
(b) z = 1.75, Area = 0.9599
(c) z = 2.42, Area = 0.9922
(d) z = -0.68, Area = 0.2483
(e) z = -1.11, Area = 0.1335