Theorem: If a random variable is normally distributed with a mean of µ and a standard deviation of σ, then the sample mean with a sample size of n would be normally distributed too with the same mean and a standard deviation of
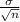
.
In this case, µ = 1200, σ = 60, sample size n = 36.
So the sample mean has a mean of 1200 and a standard deviation of
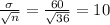
.
Then the z-score that corresponds to 1224 is