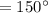Question

Triangle WXY is isosceles. ∠YWX and ∠YXW are the base angles. YZ bisects ∠WYX. m∠XYZ = (15x)°. m∠YXZ = (2x + 5)°. What is the measure of ∠WYX?

PLEASE EXPLAIN THE STEPS

A. 5°B.15°C.75° D. 150°

Answer 1

150 D

Explanation:

Answer 2

Option D is correct.

The measure of
`\angleWYX = 150^(\circ)`

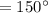
Explanation:

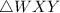`\triangle WXY` is isosceles and
`\angle YWX` and
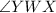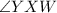`\angle YXW` are base angles.

Isosceles Triangle:

A triangle with two equal sides, and two congruent base angles that means the angles are equal

By the definition, the base angles are equal i.e,
`m\angle YWX=m\angle YXW`

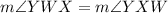
Since, YZ bisects
`m\angle WYX`

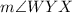
Angle Bisector theorem: An angle bisector is a line or ray that divides an angle into two equal angles

then,
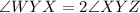`\angle WYX =2\angle XYZ` or

Substitute the value of
`\angle XYZ=(15x)^(\circ)` ;

`\angle WYX =2(15x)^(\circ) = (30x)^(\circ)`

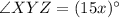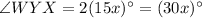
The sum of measures of these three angles of triangle WXY is equal to the 180 degree.

In triangle WXY we have;

`\angle YXW+\angle WYX+\angle YWX=180^(\circ)`

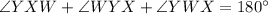
Substitute the value of
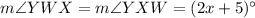`m\angle YWX=m\angle YXW=(2x+5)^(\circ)` and
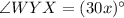`\angle WYX=(30x)^(\circ)` in above formula:

`2\angle YXW+30x=180^(\circ)` or

`2\cdot(2x+5)+30x=180^(\circ)`

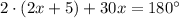
Simplify:

`4x+10+30x=180^(\circ)`

Combine like terms ;

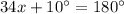`34x+10^(\circ)=180^(\circ)` or

`34x=170^(\circ)`

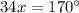
Simplify;

`x= (170)/(34) =5^(\circ)`

Substitute the value of x in
`\angle WYX`;

`\angleWYX = (30x)^(\circ) = 30 \cdot 5 = 150^(\circ)`

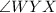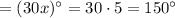
Therefore, the measure of
`\angleWYX = 150^(\circ)`