Answer:
Option 3 - (-0.7,1)
Explanation:
Given : Function
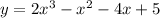
To find : Over which interval is the function decreasing?
Solution :
First we plot the graph using graphing calculator.
Refer the attached figure below.
Now, Examining the graph
From
 to (-0.667,6.63) the graph is increasing as the curve is increasing.
to (-0.667,6.63) the graph is increasing as the curve is increasing.
From (-0.667,6.63) to (1,2) the graph decreasing as the curve is decreasing.
From (1,2) to
 the graph is increasing as the curve is increasing.
the graph is increasing as the curve is increasing.
So, The interval in which the function is decreasing is given by (-0.667,1)
Round to nearest tenth, (-0.7,1)
Therefore, Option 3 is correct.