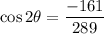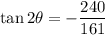Question

Pre-Cal Help!! (Image Attached)

Answer 1

To solve this type of questions, a practical way is to think of the 1.quadrant situation, that is, model the situation in right triangle trigonometry.

Check the picture.

For the moment let
`\displaystyle{ \cos\theta= (8)/(17)` (we make it positive since we are modeling using a triangle.)

Using the Pythagorean theorem, the length of the side opposite to angle
`\theta` is found to be 15 units.

We can see that the sine of theta is
`\displaystyle{ \sin\theta= (opposite \ side)/(hypotenuse)= (15)/(17)`.

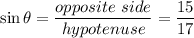
In the third quadrant, both sine and cosine of an angle are negative, so the actual values of the sine and cosine of theta are, eventually:


`\displaystyle{ \sin\theta=- (15)/(17)`,
`\displaystyle{ \cos\theta=- (8)/(17)`.

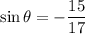
Recall the double-angle identities (formulas):


`\sin 2\theta=2\sin\theta\cos\theta`,
`\cos2\theta=cos^2(\theta)-sin^2(\theta)`.

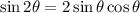
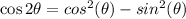
Using these identities and the ratios found above, we have:


`\displaystyle{ \cos2\theta=cos^2(\theta)-sin^2(\theta)=(- (8)/(17))^2-(- (15)/(17))^2=(64)/(289)-(225)/(289)=(-161)/(289)`

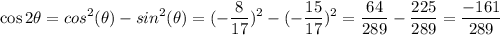
Similarly, applying the double angle formula for the sine we have:


`\displaystyle{ \sin 2\theta=2\sin\theta\cos\theta=2\cdot(- (8)/(17))(- (15)/(17))=(240)/(289)`


`\displaystyle{ \tan2\theta= (\sin 2\theta)/(\cos 2\theta)= ((240)/(289))/((-161)/(289))= -(240)/(161)`


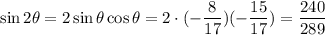
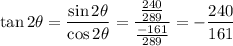
Answer:


`\displaystyle{\cos2\theta=(-161)/(289)`



`\displaystyle{ \tan2\theta= -(240)/(161)`