Question

Evaluate exactly the value of the integral from negative 1 to 0 of the product of the cube of the quantity 2 times x to the 4th power plus 8 times x and 4 times x to the 3rd power plus 4, dx. Your work must include the use of substitution and the antiderivative.

Answer 1

-162

Explanation:

Integration by substitution is a technique in calculus where a change of variables is made to simplify the integral by expressing it in terms of a new variable, making the integration easier to manage.

To evaluate the following integral, use the method of substitution:

`\displaystyle \int_(-1)^0 (2x^4 + 8x)^3 (4x^3 + 4) \;\text{d}x`

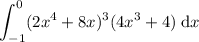
Let u = 2x⁴ + 8x.

Differentiate u with respect to x using the power rule for differentiation by multiplying each term by its exponent and then subtracting 1 from the exponent:

`\frac{\text{d}u}{\text{d}x}=4 \cdot 2x^(4-1)+1\cdot 8 x^(1-1)`

`\frac{\text{d}u}{\text{d}x}=8x^(3)+8`

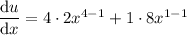
Rewrite it so that dx is on its own:

`\text{d}u=8x^(3)+8\;\text{d}x`

`\text{d}x=(1)/(8x^(3)+8)\;\text{d}u`

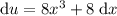
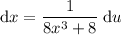
Change the limits of integration from x to u:

`\begin{aligned}x=-1 \implies u&=2(-1)^4 + 8(-1)\\&=2(1)-8\\&=2-8\\&=-6\end{aligned}`

`\begin{aligned}x=0 \implies u&=2(0)^4 + 8(0)\\&=2(0)-0\\&=0-0\\&=0\end{aligned}`

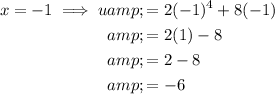
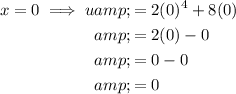
Rewrite the integral in terms of u:

`\begin{aligned}\displaystyle \int_(-1)^0 (2x^4 + 8x)^3 (4x^3 + 4) \;\text{d}x&=\int_(-6)^0 u^3 (4x^3 + 4) \cdot (1)/(8x^(3)+8)\;\text{d}u\\\\&=\int_(-6)^0 u^3 (4x^3 + 4) \cdot (1)/(2(4x^(3)+4))\;\text{d}u\\\\&=\int_(-6)^0(u^3)/(2) \;\text{d}u\end{aligned}`

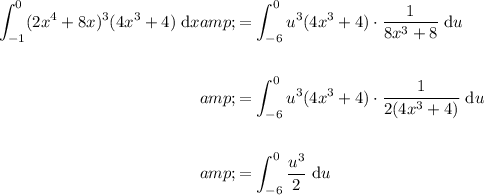
Integrate with respect to u using the power rule for integration by adding 1 to the exponent of each term and then dividing by the new exponent:

`\begin{aligned}\displaystyle \int_(-6)^0(u^3)/(2) &=\left[(u^(3+1))/(2 \cdot (3+1))\right]^0_(-6)\\\\&=\left[(u^(4))/(8)\right]^0_(-6)\\\\&=((0)^4)/(8)-((-6)^4)/(8)\\\\&=0-(1296)/(8)\\\\&=-162\end{aligned}`

Therefore, the value of the given integral is -162.

Answer 2

`\bf \displaystyle \int_(-1)^(0)~(2x^4+8x)^3(4x^3+4)\cdot dx\\\\ -------------------------------\\\\ u=2x^4+8x\implies \cfrac{du}{dx}=8x^3+8\implies \cfrac{du}{2(4x^3+4)}=dx\\\\ -------------------------------\\\\ \displaystyle \int_(-1)^(0)~u^3\underline{(4x^3+4)}\cdot \cfrac{du}{2\underline{(4x^3+4)}}\implies \cfrac{1}{2}\int_(-1)^0~u^3\cdot du\\\\ -------------------------------\\\\`


`\bf \textit{now, let's change the bounds, using }u(x)\\\\ u(-1)=2(-1)^4+8(-1)\implies u(-1)=-6 \\\\\\ u(0)=2(0)^4+8(0)\implies u(0)=0\\\\ -------------------------------\\\\ \displaystyle \cfrac{1}{2}\int_(-6)^0~u^3\cdot du\implies \left.\cfrac{1}{2}\cdot \cfrac{u^4}{4} \right]_(-6)^0\implies \left. \cfrac{u^4}{8} \right]_(-6)^0 \\\\\\\ [0]~~-~~[162]\implies -162`

notice, by changing the bounds using u(x), we do not need to substitute back the "u".