Question

Find the area of one segment formed by a square with sides of 6" inscribed in a circle.

(Hint: use the ratio of 1:1: to find the radius of the circle.)

Answer 1

check the picture below.

now, bear in mind that, we could simply get the area of the whole circle with that radius, and tease out a quarter, because the segment is just using up a quarter of the circle, because the angle made is 90°, and then subtract the triangle from that sector, and what's leftover is the segment.


`\bf \stackrel{\textit{area of the circle}}{A=\pi r^2}\implies A=\pi (3√(2))^2\implies A=\pi 3^2√(2^2)\implies A=18\pi \\\\\\ \textit{now one-quart of that is }\cfrac{18\pi }{4}\implies \cfrac{9\pi }{2}\impliedby \textit{sector's area}`


`\bf \stackrel{\textit{area of the triangle}}{A=\cfrac{1}{2}bh}\implies A=\cfrac{(3√(2))(3√(2))}{2}\implies A=\cfrac{3^2√(2^2)}{2}\\\\\\A=\cfrac{18}{2}\implies A=9\impliedby \textit{area of that triangle}\\\\ -------------------------------\\\\ \stackrel{sector's area}{\cfrac{9\pi }{2}}~~-~~\stackrel{\textit{area of the triangle}}{9}\implies \cfrac{9\pi -18}{2}\impliedby \textit{segment's area}`

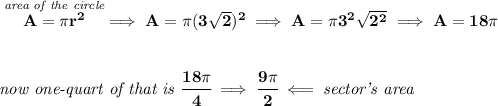
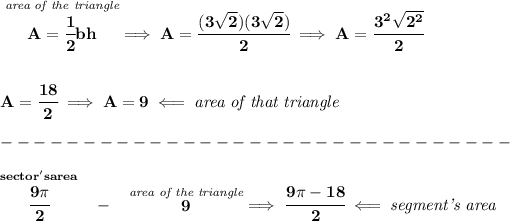
or you can always just use the area of a segment, with the radius and angle given.


`\bf \textit{area of a segment of a circle}\\\\ A=\cfrac{r^2}{2}\left[\cfrac{\theta \pi }{180}-sin(\theta ) \right] \\\\\\ \begin{cases} r=3√(2)\\ \theta =90 \end{cases}\implies A=\cfrac{(3√(2))^2}{2}\left[\cfrac{90 \pi }{180}-sin(90^o ) \right]`