Question

Problems 20 - 23. Analytically determine what type(s) of symmetry, if any, the graph of the equation would possess. Show your work.20) x^2 + 2y = 7 21) y^2 - xy = 622) x^2 + y^2 =3|x|

Answer 1

ANSWER and EXPLANATION

We want to test for symmetry for the given function:

`\begin{gathered} x^2\text{ + 2y = 7} \\ \Rightarrow\text{ y = }(1)/(2)(7-x^2) \end{gathered}`

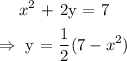
The function can be symmetric:

=> about the y axis

=> about the x axis

=> about the origin

ABOUT Y AXIS

To test for this, we replace x with -x and see if the function is the same as the original:

`\begin{gathered} y\text{ = }(1)/(2)(7-(-x)^2) \\ \Rightarrow y\text{ = }(1)/(2)(7-x^2) \end{gathered}`

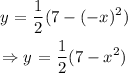
Since the equation is the same as the original, then it is symmetrical about the y axis.

ABOUT X AXIS

To test for this, we replace y with -y and see if the function is the same as the original:

`\begin{gathered} \Rightarrow\text{ -y = }(1)/(2)(7-x^2) \\ \text{Divide through by -1:} \\ \Rightarrow\text{ y = }(-1)/(2)(7-x^2) \end{gathered}`

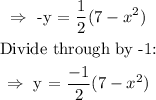
Since this is not the same as the original, it is not symmetrical about the x axis.

ABOUT THE ORIGIN

For this test, we have to replace y with -y and x with -x and then check if the function is the same as the original. It is a combination of the two above.

Since we already saw above that replacing y with -y shows that it is not symmetric about the y axis, we can conclude that it is also not symmetric about the origin.

Therefore, the graph of the equation possesses a symmetry about the y axis.