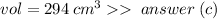Question

Find the volume of the composite solid. Round your answer to the nearest hundredth.

A.239.24cm^3
B.246.08cm^3
C.294.03cm^3
D.308.78cm^3

Answer 1

So the composite solid has a rectangular pyramid top with a rectangular box below.
We can find the total vol. by adding the two together: Vol (v)total = vol (pyra) + vol (box)
vol (tot) = (1/3×base×height) + (l×w×h)
In order to find the height (h) of the triangle, we imagine a string dropped straight down from the apex (tip), which falls perfectly to center of the base of pyramid. Now the distance from the bottom of that string to edge is 1/2×6.7 = 3.35. Use Pythagorean Theorem to determine the pyramid height:

`{5.8}^(2) = {h}^(2) + {3.35}^(2) \\ {h}^(2) = {5.8}^(2) - {3.35}^(2) \\ h \: = \sqrt{({5.8}^(2) - {3.35}^(2))} \\ h = √((33.64 - 11.22)) \\ h = √(22.42) = 4.73 \: cm`
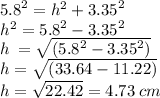
Now we can solve our volume, so the base of pyra = l×w = 6.2×6.7 = 41.54
vol (tot) = (1/3×base×height) + (l×w×h)
vol = (1/3×41.54×4.73) + (6.7×6.2×5.5)
vol = (65.49) + (228.47) = 293.96

`vol = 294 \: {cm}^(3) > > \: answer \: (c)`