Question

Find the work done by the force field f(x, y, z) = y + z, x + z, x + y on a particle that moves along the line segment from (1, 0, 0) to (5, 3, 2).

Answer 1

Note that the vector field is irrotational, since


`\\abla*\mathbf f(x,y,z)=\mathbf 0`

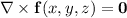
which means
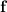
`\mathbf f` is conservative. This means there is some scalar potential function
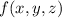
`f(x,y,z)` such that
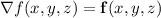
`\\abla f(x,y,z)=\mathbf f(x,y,z)`. If we can find such a function, then we only need to evaluate the difference of
`f(5,3,2)` and
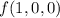
`f(1,0,0)` (because the gradient theorem holds in this case).

We're looking for a function
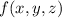
`f(x,y,z)` that satisfies


`(\partial f)/(\partial x)=y+z`

`(\partial f)/(\partial y)=x+z`

`(\partial f)/(\partial z)=x+y`

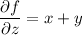
Integrate the first equation with respect to
`x` to get


`f(x,y,z)=xy+xz+g(y,z)`

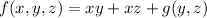
Differentiate with respect to
`y`, then we must have


`(\partial f)/(\partial y)=x+z=x+(\partial g)/(\partial y)`

`\implies(\partial g)/(\partial y)=z`

`\implies g(y,z)=yz+h(z)`

`\implies f(x,y,z)=xy+xz+yz+h(z)`

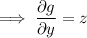
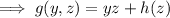
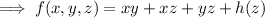
Differentiate with respect to
`z`, and we have to have


`(\partial f)/(\partial z)=x+y=x+y+(\mathrm dh)/(\mathrm dz)`

`\implies(\mathrm dh)/(\mathrm dz)=0`

`\implies h(z)=C`

`\implies f(x,y,z)=xy+xz+yz+C`

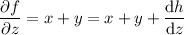
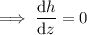
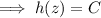
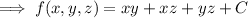
Now, by the gradient theorem, we have


`\text{work}=\displaystyle\int_(\mathcal C)\mathbf f\cdot\mathrm d\mathbf r=f(5,3,2)-f(1,0,0)=31`

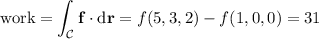
where
`\mathcal C` is the line segment.