Question

The graph of g(x) is obtained by reflecting the graph of f(x)=4|x| over the x-axis.

Which equation describes  g(x)

?

 

g(x)= | x+4 | g(x)= |x| −4 g(x)= | x−4 | g(x)=−4 |x|

Answer 1

I believe the answer is g(x) = -4|x| , because the negative changes the direction of the slope.

Answer 2

Option D

Explanation:

The given function is

`f(x)=4|x|`

It is given that the graph of g(x) is obtained by reflecting the graph of f(x)=4|x| over the x-axis.

If a figure reflected across x-axis, then the rule of reflection is

`(x,y)\rightarrow (x,-y)`

Using the above rule, if the given function reflected across x-axis, then g(x)=-f(x).

`g(x)=-(4|x|)`

`g(x)=-4|x|`

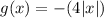
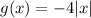
The equation g(x)=-4|x| describes g(x).

Therefore, the correct option is D.