Answer:
The values of x are
 and 1.
and 1.
Explanation:
Given quadratic function
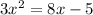
We have to solve for x.
Consider the given quadratic function
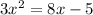
This can be written as
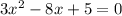
We can solve the above quadratic equation using middle term split method,
-8x can be written as -3x - 5x
Thus, the equation becomes,
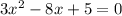

Taking 3x common from first two term and -5 common from last two terms, we get,
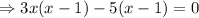
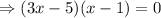
Now using zero product property
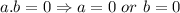 , we have,
, we have,
 or
or

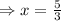 or
or
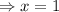
Thus, The values of x are
 and 1.
and 1.