Question

Using the rule of 72, mc003-1.jpg, how long will it take for the principal to double with an annual compound interest rate of 6%?

6 years

9 years

12 years

15 years

Answer 1

The answer is C. 12 years because i just took the test on edgenuity

Answer 2

Option C. 12 years

Explanation:

Let principal amount taken = x

We know the formula of compound interest

Final amount = Principal amount×
`(1+(r)/(n))^(nt)`

Where r = rate of interest (per year)

n = number of times compounded (annually)

t = time in years (years)

Here we have to find the time in which principal amount is doubled.

From the question r = 6% = .06

n = 1

Principal amount = P

Final amount = 2P

Now we put these values in the formula

`2P=P(1+.06)^(t)`

`2=(1.06)^(t)`

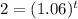
Now we take log on both the sides

`log(2)=log(1.06)^(t)`

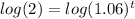
0.301 = tlog(1.06)

0.301 = t×(.025)

`(0.301)/(0.25)=t`

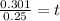
t = 12 years.

Option C. 12 years is the answer.