Question

At a canning company the daily production cost, y, is given by the quadratic equation y = 650 – 15x + 0.45x2, where x is the number of canned items. What is the MINIMUM daily production cost?

A) $1,025.00 B) $1,186.25 C) $525.00 D) $536.25

Answer 1

The equation is a parabola so the minimum point is the vertex.

(-b/2a, y)

x = 15/0.9 = 16.67 canned itemz
y = 524.95 $

So it's C.

Answer 2

Option C) is correct

Explanation:

Given : y is the daily production cost at a canning company such that
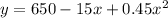`y=650-15x+0.45x^2` wherex is the number of canned items .

To find : Minimum daily production cost

Solution :

`y=650-15x+0.45x^2`

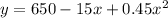
On differentiating both sides with respect to x, we get

`\frac{\mathrm{d} y}{\mathrm{d} x}=-15+0.9x`

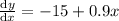
On putting
`\frac{\mathrm{d} y}{\mathrm{d} x}=0` , we get
`-15+0.9x=0\Rightarrow 15=0.9x\Rightarrow x=(15)/(0.9)=(150)/(9)=(50)/(3)`

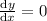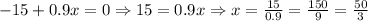
We get intervals as \left ( -\infty , \frac{50}{3}\right )\,,\,\left ( \frac{50}{3},\infty \right )
`\left ( -\infty , (50)/(3)\right )\,,\,\left ( (50)/(3),\infty  \right )`

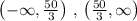
For
`x=0\epsilon \left ( -\infty ,(50)/(3) \right )` ,
`f'(0)=-15< 0`

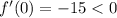
For
`x=16\epsilon \left ( (50)/(3),\infty  \right )` ,
`f'(18)=-15+0.9(18)=-15+16.2=1.2> 0`

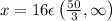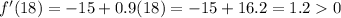
Therefore,
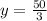`y=(50)/(3)` is a point of minima.

So, minimum cost is equal to
`y\left ( (50)/(3) \right )`

`y\left ( (50)/(3) \right )=650-15\left ( (50)/(3) \right )+0.45\left ( (50)/(3) \right )^2=650-250+125=\$ 525`

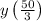
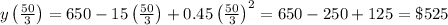
So, option C) is correct .