ANSWER
Perimeter: 88.3 cm
Area: 375 cm²
Step-by-step explanation
Since this is an isosceles triangle its height divides the triangle into two equal right triangles. Therefore, to find the length of the congruent sides, we can use the Pythagorean theorem:
a is the hypotenuse of the triangle and the legs are 25cm and 15cm:
![\begin{gathered} a^2=25^2+15^2 \\ a=\sqrt[]{625+225} \\ a=\sqrt[]{850} \\ a=5\sqrt[]{34} \\ a\approx29.16\operatorname{cm} \end{gathered}]()
The perimeter is the sum of the side lengths:
![P=a+a+(15\operatorname{cm}+15\operatorname{cm})=29.16\operatorname{cm}+29.16\operatorname{cm}+30\operatorname{cm}=88.32\operatorname{cm}\approx88.3\operatorname{cm}]()
The area of a triangle is:
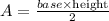
In this triangle the base is 30cm (