Question

What is the equation of the axis of symmetry of the graph of y + 3x – 6 = –3(x – 2)2 + 4?

A. x=3/2
B. x=-1/6
C. x=-1/2
D. x=-3/2

Answer 1

What is the equation of the axis of symmetry of the graph of y + 3x – 6 = –3(x – 2)2 + 4?


A. x=3/2

Answer 2

Option: A is the correct answer.

The axis of symmetry is:

A. x=3/2

Explanation:

We are given a graph as:

`y+3x-6=-3(x-2)^2+4`

and

`y=-3(x-2)^2+4+6-3x`

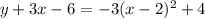
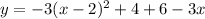
and

`y=-3[(x-2)^2+x]+10\\\\i.e.\\\\y=-3[x^2+4-4x+x]+10\\\\i.e.\\\\y=-3[x^2-3x+4]+10`

This equation could also be written in the form:

`y=-3[x^2-3x+4-(9)/(4)+(9)/(4)]+10\\\\i.e.\\\\y=-3[(x-(3)/(2))^2+4-(9)/(4)]+10\\\\i.e.\\\\y=-3[(x-(3)/(2))^2+(7)/(4)]+10\\\\i.e.\\\\y=-3(x-(3)/(2))^2-3* (7)/(4)+10\\\\i.e.\\\\y=-3(x-(3)/(2))^2+(19)/(4)`

Now, we know that for any general equation of the type:

`y=a(x-h)^2+k`

The axis of symmetry of the graph of the equation is:

`x=h`

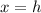
Here we have:

`h=(3)/(2)`

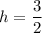
Hence, the answer is: Option: A