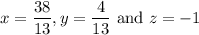Question

What is the solution to the system of equation?

-3x-4y-32= -7
2x-6y+2=3
5x-2y+5z=9

Answer 1

Simplifying 8x + 336 = 336 + -3x Reorder the terms: 336 + 8x = 336 + -3x Add '-336' to each side of the equation. 336 + -336 + 8x = 336 + -336 + -3x Combine like terms: 336 + -336 = 0 0 + 8x = 336 + -336 + -3x 8x = 336 + -336 + -3x Combine like terms: 336 + -336 = 0 8x = 0 + -3x 8x = -3x Solving 8x = -3x Solving for variable 'x'. Move all terms containing x to the left, all other terms to the right. Add '3x' to each side of the equation. 8x + 3x = -3x + 3x Combine like terms: 8x + 3x = 11x 11x = -3x + 3x Combine like terms: -3x + 3x = 0 11x = 0 Divide each side by '11'. x = 0 Simplifying x = 0

Answer 2

`x=(38)/(13),y=(4)/(13)\text{ and }z=-1`

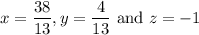
Explanation:

we are given three equation of variable x, y and z.

-3x-4y-3z= -7 ------------- (1)

2x-6y+z=3 ------------- (2)

5x-2y+5z=9 ------------- (3)

• Using elimination method to eliminate z from equation (1) and (2)

Make the coefficient of z same in both equation.

Multiply equation (2) by 3

-3x - 4y - 3z = -7

6x - 18y + 3z = 9

Add above equation to eliminate z

3x - 22y = 2 ---------------(4)

• Using elimination method to eliminate z from equation (2) and (3)

Make the coefficient of z same in both equation.

Multiply equation (2) by -5

-10x + 30y - 5z = -15

5x - 2y + 5z = 9

Add above equation to eliminate z

-5x + 28y = -6 ---------------(5)

• Using elimination method to eliminate x from equation (4) and (5)

Make the coefficient of x same in both equation.

Multiply equation (4) by 5 and equation (5) by 3

15x - 110y = 10

-15x + 84y = -18

Add above equation to eliminate x

-26y = -8

`y=(4)/(13)`

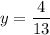
Substitute y into equation (5) to get x

So,
`-5x+28((4)/(13))=-6`

`x=(38)/(13)`

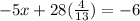
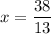
Substitute x and y into equation (1)

`-3\cdot (38)/(13)-4\cdot (4)/(13)-3z=-7`

`z=-1`

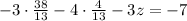
Solution:

`x=(38)/(13),y=(4)/(13)\text{ and }z=-1`