Question

In triangle ABC, side AB has a length of 8 cm and side BC has a length of 5 cm. If the triangle has an area of 10 square centimeters, what is the measure of the angle between sides AB and BC?

135°
150°
120°
45°
30°
60°

Thank you!

Answer 1

Recall the following formula:

Given a triangle with side lengths a, b, and c. Let the measure of the angle between sides of length a and c be B.

Then, the area of the triangle is given by :


`Area= (1)/(2)\cdot a\cdot c \cdot \sin B`.

In our example we have: Area=10 square cm, a=8 cm, c=5 cm, and we want to find the measure of the angle between the 2 sides a and c.

Substituting in the formula we have:


`10= (1)/(2)\cdot 8\cdot 5 \cdot \sin B`

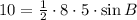
Thus,
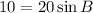
`10=20 \sin B`, which means
`\sin B = (1)/(2)`.


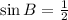
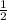
`(1)/(2)` is the sine of
`30^(\circ)`, but also
`150^(\circ)`.


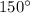
Answer: both 30, and 150 degrees are possible