Question

Select all the points that lie on a circle with a center at (3,-5) and a radius of 7.A. (-2, -3)B. (3,-5)C. (3,2)D. (10,-5)E. (10,2)

Answer 1

Given :

Circle with center : (3, -5)

radius : 7

The equation of a circle with center (a,b) and radius r is given as :

`(x-a)^2+(y-b)^2=r^2`

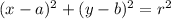
The equation of the circle with center (3, -5) and radius 7 is :

`\begin{gathered} (x-3)^2+(y+5)^2=7^2 \\ (x-3)^2+(y+5)^2\text{ = 49} \end{gathered}`

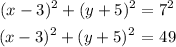
The points that lie on the circle can be found by substituting the points into the equation

for (-2, -3)

`\begin{gathered} (-2-3)^2+(-3+5)^2\text{ } \\ 29\text{ }\\e\text{ 49} \end{gathered}`

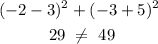
for (3, -5)

`\begin{gathered} (3-3)^2+(-5+5)^2 \\ 0\text{ }\\e\text{ 49} \end{gathered}`

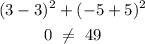
for (3,2)

`\begin{gathered} (3-3)^2+(2+5)^2 \\ \text{ 49 = 49} \end{gathered}`

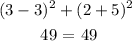
For (10, -5)

`\begin{gathered} (10-3)^2+(-5+5)^2\text{ } \\ 49\text{ = 49} \end{gathered}`

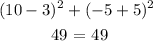
for (10, 2)

`\begin{gathered} (10-3)^2+(2+5)^2 \\ 98\\e49\text{ } \end{gathered}`

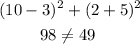
Hence, the points that lie on a circle are : (3,2) and (10, -5)