Question

Related Rates Problem: The radius of a spherical watermelon is growing at a constant rate of 2 centimeters per week. The thickness of the rind is always one tenth of the radius. The volume of the rind is growing at the rate __?__ cubic centimeters per week at the end of the fifth week. Assume that the radius is initially zero. ...?

Answer 1

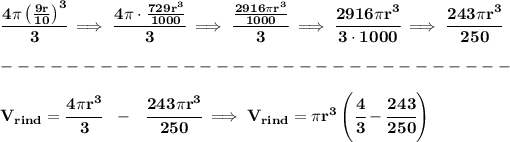
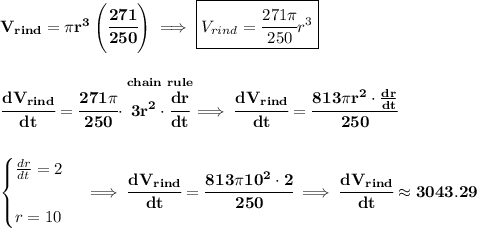
check the picture below.

so, if we grab the whole volume of the watermelon, and then subtract the volume of the inner sphere of 9/10, what we're left with is 1/10 of the volume, which is the volume of the rind, recall the rind has a radius of 1/10 of the radius, so we're simply taking off 1/10 from the radius and using the 9/10 and subtracting the volume with that radius.

now, after the 5th week, the radius of the watermelon has then grown to 2*5, or 10 cm, and the rind is 1/10 of that or just 1 cm.


`\bf \cfrac{4\pi \left( (9r)/(10) \right)^3}{3}\implies \cfrac{4\pi \cdot (729r^3)/(1000)}{3}\implies \cfrac{(2916\pi r^3)/(1000)}{3}\implies \cfrac{2916\pi r^3}{3\cdot 1000}\implies \cfrac{243\pi r^3}{250}\\\\ -------------------------------\\\\ V_(rind)=\cfrac{4\pi r^3}{3}~~-~~\cfrac{243\pi r^3}{250}\implies V_(rind)=\pi r^3\left(\cfrac{4}{3}-\cfrac{243}{250} \right)`


`\bf V_(rind)=\pi r^3\left( \cfrac{271}{250}\right)\implies \boxed{V_(rind)=\cfrac{271\pi }{250}r^3} \\\\\\ \cfrac{dV_(rind)}{dt}=\cfrac{271\pi }{250}\cdot \stackrel{chain~rule}{3r^2\cdot \cfrac{dr}{dt}}\implies \cfrac{dV_(rind)}{dt}=\cfrac{813\pi r^2\cdot (dr)/(dt)}{250} \\\\\\ \begin{cases} (dr)/(dt)=2\\\\ r=10 \end{cases}\implies \cfrac{dV_(rind)}{dt}=\cfrac{813\pi 10^2\cdot 2}{250}\implies \cfrac{dV_(rind)}{dt}\approx 3043.29`