Question

Find the slope of a line parallel to 3x+5y=15

Answer 1

the answer is negative three over five

Answer 2

A.
`-(3)/(5)`.

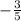Explanation:

We have been given equation of a line
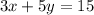`3x+5y=15`. We are asked to find the slope of a parallel line to our given line.

We know that slopes of parallel lines are equal, so slope of the parallel line will be equal to slope of our given line.

To find the slope of our given line, we will convert our given equation in slope-intercept form of equation
`y=mx+b`, where m represents slope of line.

First of all, we will subtract 3x from both sides of our given equation as:

`3x-3x+5y=15-3x`

`5y=-3x+15`

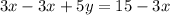
Now, we will divide both sides by 5.

`(5y)/(5)=(-3x+15)/(5)`

`y=(-3x)/(5)+(15)/(5)`

`y=-(3x)/(5)+3`

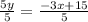
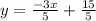
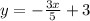
Upon comparing our equation with slope-intercept form, we can see that
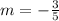`m=-(3)/(5)` and option A is the correct choice.