For this exercise, let's check every option given in the picture:
Option A
Given:
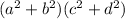
Simplify it by solving the multiplication:
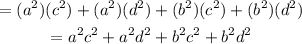
Notice that the expression given in the exercise as the product is:
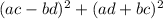
Îf you simplify it, you get:
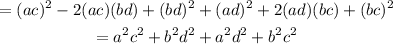
Therefore:
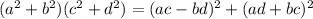
Option B
Apply the same steps used in Option A. Then:
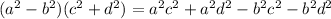
Simplify the result given in the exercise :
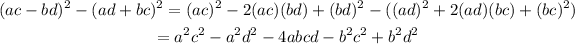
Compare it with the one found above:
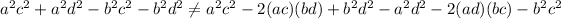
Option C
Applying the same procedure, you get:
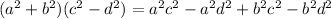
Simplify the result shown in the picture:
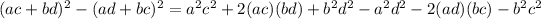
Notice that:
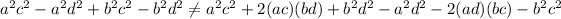
Option D
You already know that:
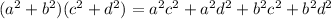
Simplify the result given in the exercise:
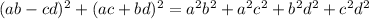
Then:
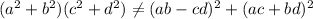
The answer is: OptionA.