Question

A boat is heading towards a lighthouse, whose beacon-light is 113 feet above thewater. From point A, the boat's crew measures the angle of elevation to the beacon,10°, before they draw closer. They measure the angle of elevation a second time frompoint B at some later time to be 21°. Find the distance from point A to point B.Round your answer to the nearest foot if necessary.

Answer 1

The following picture represents an explanation to the given question:

CD represents the beacon

We need to find the distance AB

The measure of the angle C = 90

At the triangle BCD,

The measure of the angle CDB = 90 - 21 = 69

Using the sine law, we will find the length of BD

So,

`\begin{gathered} (BD)/(\sin90)=(CD)/(\sin 21) \\ BD=CD\cdot(\sin90)/(\sin21)=(CD)/(\sin 21) \end{gathered}`

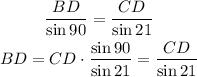
At the triangle ABC

The measure of the angle CDA = 90 - 10 = 80

So, the measure of the angle ADB = angle CDA - angle CDB = 80 - 69 = 11

At the triangle ADB, using sin law:

`\begin{gathered} (AB)/(\sin D)=(BD)/(\sin A) \\ \\ AB=BD\cdot(\sin D)/(\sin A)=BD\cdot(\sin 11)/(\sin 10) \end{gathered}`

substitute with the value of BD and CD s

So,

`AB=(CD)/(\sin21)\cdot(\sin11)/(\sin10)=(113\cdot\sin 11)/(\sin 21\cdot\sin 10)=346.4798`

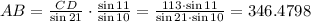
Rounding the answer to the nearest foot

So, the answer will be AB = 346 ft