Solution:
The given function is:
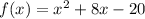
To identify the zeros of the function, substitute x = 0 in each given function if they give the same constant term as in the original function then that function is rewritten of the given function.
First, put x =0 in the original function gives:
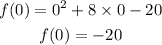
Now, if the functions given in the option give the same constant -20 after putting x = 0 then that function can be rewritten of the original function.
In option A
Put x = 0, it gives:
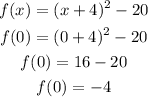
This function gives -4.
Thus, option A is not correct.
In option B,
Put x = 0, it gives:
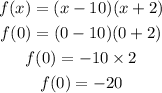
Therefore, option B is correct.
In option C
Put x = 0, it gives:
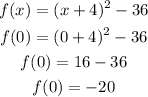
Therefore, option C is also correct.
In option D,
Put x = 0, it gives:
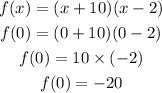
Therefore, option D is also correct.
Hence, the correct options are B, C, D.