Answer:
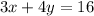
Explanation:
Given equation of a line =
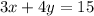
i.e.

i.e.
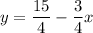
i.e.
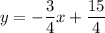 (1)
(1)
It is in intercept form
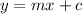 (2) , where m is slope.
(2) , where m is slope.
By comparing (1) and (2) the slope of line :
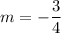
Also the parallel lines have same slope .
The equation of a line passing through a point (a,b) and having a slope of 'm' is given by :-
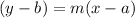
Then the equation of the line that passes through (8,-2) and having slope of
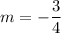 is given by :-
is given by :-
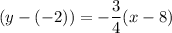

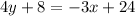

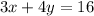
Hence , the equation of a line that passes through the point (8, −2) and is parallel to the line whose equation is
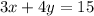 is
is
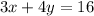
.