Let's draw a vertical line on the coordinate plane:
we have that the vertical line passes through the points (x,y_1) and (x,y_2). So if we want to find the slope this would happen:
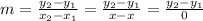
So, we have that a vertical line have undefined slope since the denominator becomes 0 when we calculate the slope.
Now for the horizontal line, we have the following:
If we calculate the slope we get the following:
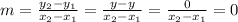
As we can see, the slope of a horizontal line is 0 since the values of the numerator become 0, and that is defined as a real number.