Question

1. Consider the following diagram. geri Pat A: Which of the following statements is enough to prove that ABCD is a kite but not any other quadrilateral? A ABCD has at least one pair of congruent opposite angles. B Not all four sides of ABCD are equal, but there are two palrs of equal adjacent sides. C The dlagonals of ABCD are perpendicular to each other. D The diagonals of ABCD fom four right triangles. Part B: Complete the following statement. IF ABCD is a kite, EB is 24 meters long, EC Is 10 meters long, and EA IS B0 meters long, the perimeter of ABCD measures meters and the area of ABCD measures square meters.

Answer 1

We have the following:

We know that a quadrilateral is that it has four sides, but in this case the most important thing is that the comet is formed by triangles, in the other quadrilaterals it is formed by other quadrilaterals (squares or rectangles)

Therefore the correct answer is D

The perimeter is the sum of all the sides, therefore:

`\begin{gathered} p=AD+AB+DC+BC \\ AD=AB \\ AD=\sqrt[]{EB^2+EA^2} \\ EB=24 \\ EA=80 \\ AD=\sqrt[]{24^2+80^2} \\ AD=\sqrt[]{576+6400}=\sqrt[]{6976}=83.52 \\ DC=BC \\ BC=\sqrt[]{EB^2+EC^2} \\ EB=24 \\ EC=10 \\ BC=\sqrt[]{24^2+10^2} \\ BC=\sqrt[]{24^2+10^2}=\sqrt[]{576+100}=\sqrt[]{676}=26 \\ p=AD+AB+DC+BC=83.52+83.52+26+26 \\ p=219.04 \end{gathered}`

The perimeter is 219.04 meters

Now, for the area:

The area of a kite is the horizontal side by the vertical side, divided by two

`\begin{gathered} A=(XY)/(2) \\ X=AE+EC=80+10=90 \\ Y=ED+EB=24+24=48 \\ A=(90\cdot48)/(2)=2160 \end{gathered}`

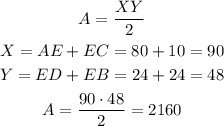
Therefore the area is 2160 square meters