Question

G verify that the divergence theorem is true for the vector field f on the region

e. f(x, y, z) = z, y, x , e is the solid ball x2 + y2 + z2 ≤ 36

Answer 1

`\mathbf f(x,y,z)=\langle z,y,x\rangle\implies\\abla\cdot\mathbf f=(\partial z)/(\partial x)+(\partial y)/(\partial y)+(\partial x)/(\partial z)=0+1+0=1`

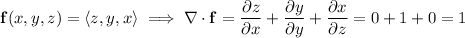
Converting to spherical coordinates, we have


`\displaystyle\iiint_E\\abla\cdot\mathbf f(x,y,z)\,\mathrm dV=\int_(\varphi=0)^(\varphi=\pi)\int_(\theta=0)^(\theta=2\pi)\int_(\rho=0)^(\rho=6)\rho^2\sin\varphi\,\mathrm d\rho\,\mathrm d\theta\,\mathrm d\varphi=288\pi`

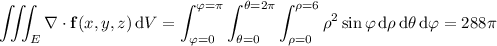
On the other hand, we can parameterize the boundary of
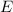
`E` by


`\mathbf s(u,v)=\langle6\cos u\sin v,6\sin u\sin v,6\cos v\rangle`

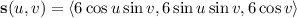
with
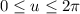
`0\le u\le2\pi` and
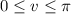
`0\le v\le\pi`. Now, consider the surface element


`\mathrm d\mathbf S=\mathbf n\,\mathrm dS=(\mathbf s_v*\mathbf s_u)/(\|\mathbf s_v*\mathbf s_u\|)\|\mathbf s_v*\mathbf s_u\|\,\mathrm du\,\mathrm dv`

`\mathrm d\mathbf S=\mathbf s_v*\mathbf s_u\,\mathrm du\,\mathrm dv`

`\mathrm d\mathbf S=36\langle\cos u\sin^2v,\sin u\sin^2v,\sin v\cos v\rangle\,\mathrm du\,\mathrm dv`

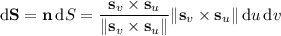
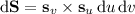
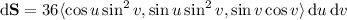
So we have the surface integral - which the divergence theorem says the above triple integral is equal to -


`\displaystyle\iint_(\partial E)\mathbf f\cdot\mathrm d\mathbf S=36\int_(v=0)^(v=\pi)\int_(u=0)^(u=2\pi)\mathbf f(x(u,v),y(u,v),z(u,v))\cdot(\mathbf s_v*\mathbf s_u)\,\mathrm du\,\mathrm dv`

`=\displaystyle36\int_(v=0)^(v=\pi)\int_(u=0)^(u=2\pi)(12\cos u\cos v\sin^2v+6\sin^2u\sin^3v)\,\mathrm du\,\mathrm dv=288\pi`

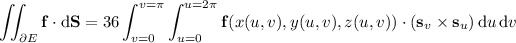
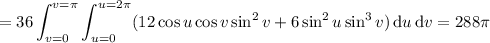
as required.