Question

How to find the equation of an exponential function given two points?

Answer 1

An exponential function is given by
`y=a(b)^x`

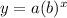
Given two points, (m, n) and (p, q), we find the equation of the exponential function as follows:


`n=a(b)^m \ .\ .\ .\ (1) \\ \\ q=a(b)^p \ .\ .\ .\ (2) \\ \\ ((1))/((2)) \Rightarrow (n)/(q) = (b^m)/(b^p) =b^(m-p) \\ \\ \Rightarrow \ln\left( (n)/(q) \right)=(m-p)\ln(b) \\ \\ \Rightarrow \ln(b)= (\ln\left( (n)/(q) \right))/(m-p) \\ \\ \Rightarrow b=e^{(\ln\left( (n)/(q) \right))/(m-p)`

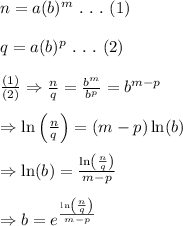
From (1), we have:


`n=a\left(e^{m(\ln\left( (n)/(q) \right))/(m-p)\right) \\ \\ \Rightarrow a= \frac{n}{\left(e^{m(\ln\left( (n)/(q) \right))/(m-p)\right)}}`

Therefore, the equation of an exponential function given two points (m, n) and (p, q) is given by


`y=\frac{n}{\left(e^{m(\ln\left( (n)/(q) \right))/(m-p)\right)}}\left(e^{(\ln\left( (n)/(q) \right))/(m-p)\right)^x`

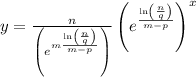
[i.e. you can choose any set of points and substitute the values in the equation above to get the exponential equation]