Question

The equation of circle is O(x - 3)2 + (y + 5)2 = 16Circle O' is the image of circle 0 after translation 5 left and 6 up.Circle O" is the image of circle O' after dilation centered at the origin with the scalefactor of 3Center of circle O' isradius of circle O'isCenter of circle O" isradius of circle O" isEquation of circle O" is

Answer 1

Step 1

Using the given translations, find the equation for circle O'

`\begin{gathered} \text{ To translate the original circle to the left by 5 units, we add 5 to x} \\ \text{To translate the original circle up by 6 units, we subtract 6 from y} \\ \text{ Hence} \\ \text{The equation of the circle O after transformation becomes is } \\ O^(\prime)\colon(x+2)^2+(y-1)=16 \end{gathered}`

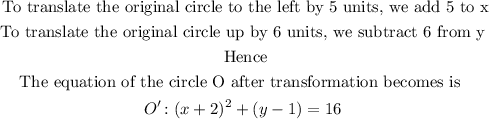
That is the equation of circle O' becomes

`O^(\prime)=(x+2)^2+(y-1)=16`

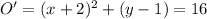
From the image the green circle is that of circle O and the blue circle is that of circle O'

Equation of the new circle is

(x + 2)² + (y - 1)² = 16

Step 1: Dilate the circle O' by a scale factor of 3 to get a new circle O"

To dilate the circle O', we multiply the right side of the equation of circle O' by 3² to get:

`O^(\doubleprime)=(x+2)^2+(y-1)=3^2*16=9*16`

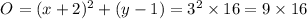
Equation of the new circle after dilation becomes

O": (x + 2)² + (y - 1)² = 144