Let the planes speed = x
And the wind speed = y
The distance = 180 miles
Speed = distance over the time
On the go :
Time = 2 hours
so,
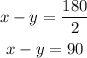
On the way back, the wind is still blowing at the same speed so the return trip takes only 1 hour and 30 minutes.
Time = 1.5 hours
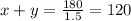
so, we have the following system of equations:
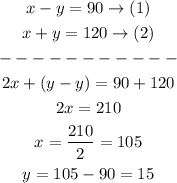
So, the answer is:
his plane speed equals 105 mph
the wind speed equals 15 mph