Question

Which linear inequality is represented by the graph?y ≤ x − 1y ≥ x − 1y < 3x − 1y > 3x − 1

Answer 1

Solution: As the line shown in the graph passes through (3,0) and (0,-1).

So, equation of line passing through (3,0) and (0,-1) is given by two point formula i.e equation of line passing through (p,q) and (a,b) is given by

→
`(y-q)/(x-p)=(q-b)/(p-a)`

→
`(y-0)/(x-3)=(0+1)/(3-0)`

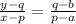
So ,the equation of line is ,→3 y = x-3

→ x- 3 y -3= 0 or y=x/3 -1

take point (0,0) and putting in the above equation, we see that ,L.H.S>R.H.S

Similarly if you take other points , like (1,0).(0,1) we see that ,L.H.S>R.H.S.

it means the above equation can be written as , y≥x/3 -1.

None of the option is correct.

Answer 2

First, work out the equation of the graph.
Equation of a straight line graph is given in the form
`y = mx+c` where
`m` is the slope of the line and
`c` is the y-intercept.

The graph given shows the line intercept y-axis at (0, -1)

To work out the slope, choose any two coordinates then find their vertical and horizontal distance. Say we choose (0, -1) and (3, 0)
The vertical distance is 1 and the horizontal distance is 3, so the slope is

`m = (-1-0)/(0-3)= (-1)/(-3)= (1)/(3)`

Then form the equation for the line

`y=mx+c`

`y= (1)/(3)x-1`→ Multiply each term by 3

`3y = x - 3`

Now the inequality part, the shaded region is above the line, so the values intended are 'greater than' and the line is a bold line, so the inequality is 'greater than or equal to' and the symbol is ≥

The inequality is then
3y ≥ x - 3

Note: None of the options show this answer. Maybe check if the original options have been copied correctly.