Find the equation of the parable in general form by completing the square. Then, state its vertex x^(2) +2x-y+3=0

Question

Find the equation of the parable in general form by completing the square. Then, state its vertex


`x^(2) +2x-y+3=0`

Answer 1

The parabola will show the vertex in the format: y-k = (x-h)^2, where the vertex point
lies at (h, k).

`so \: for \: {x}^(2) + 2x - y + 3 = 0`
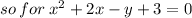
let's first put it in "y =" standard format:

`y = {x}^(2) + 2x + 3`
Since we cannot get a perfect square out of this, we complete the square: a=1, b=2, c=3
(b/2)^2 = (2/2)^2 = 1, so

`y = {(x +1)}^(2) ...\: is \: y = {x}^(2) + 2x + 1`
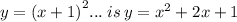
So there's +2 leftover, since 3-1=2; so:

`y = {(x + 1)}^(2) + 2`
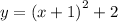
Now we'll subtract the 2 from both sides to show our vertex:

`y - 2 = {(x + 1)}^(2)`
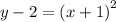
where our vertex (h, k) is at (-1, 2)