In the figure, BC and AD are line segments. What is the sum of x and y?

Question

asked Jun 17, 2018 175k views

2 Answers

Clevison Luiz · Answer 1 · 2018-06-22T21:44:43+0000

Answer:

The correct option is 2.

Explanation:

Given information: BC and AD are line segments.

According to the angle sum property, the sum of interior angles of a triangle is 180°.

In triangle DOC,

$\angle C+\angle COD+\angle D=180^(\circ)$

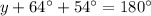
$y+64^(\circ)+54^(\circ)=180^(\circ)$

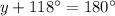
$y+118^(\circ)=180^(\circ)$

$y=180^(\circ)-118^(\circ)$

$y=62^(\circ)$

The value of y is 62°.

If two lines intersect each other then vertical opposite angles are equal.

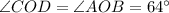
$\angle COD=\angle AOB=64^(\circ)$

In triangle AOB,

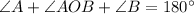
$\angle A+\angle AOB+\angle B=180^(\circ)$

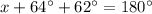
$x+64^(\circ)+62^(\circ)=180^(\circ)$

$x+126^(\circ)=180^(\circ)$

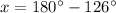
$x=180^(\circ)-126^(\circ)$

$x=54^(\circ)$

The value of x is 54°.

The sum of x and y is

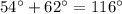
$54^(\circ)+62^(\circ)=116^(\circ)$

The sum of x and y is 116°. Therefore the correct option is 2.